|
Das, in den
Kapiteln 1 bis 7, behandelte „Spezielle
Grundmodell“ kann auch auf nicht
sonnenähnliche Systeme übertragen werden.
Gleichung 1.4.1 für sonnenähnliche Sternsysteme
lässt sich verallgemeinern, so dass sie für beliebige
Sternenmengen einer Spektralklasse in der Galaxie
gilt. |
Bezogen
auf alle Sternsysteme A in unserer
Galaxie ergibt sich die Anzahl NX
einer Menge von Sternsystemen, mit:
| 8.1.1 Gleichung |
Nx
= A·FX |
FX ist dabei
die Wahrscheinlichkeit für das Auftreten einer Menge von
Sternen, die eine bestimmte Eigenschaft
besitzen.
Eine natürliche Ordnung der Sterne ist durch das System
der Spektralklassen gegeben. Wobei im
Speziellen Grundmodell ja schon die Spektralklasse der
G-Sterne benutzt wurde.
Gleichung 8.1.1 gilt somit für die Sternenmenge einer
beliebigen Spektralklasse. (siehe auch Kapitel 12.1)
Damit lässt sich das bisher abgeleitete Konzept auf alle
Sternenmengen anwenden, für die Beobachtungsdaten
vorliegen.
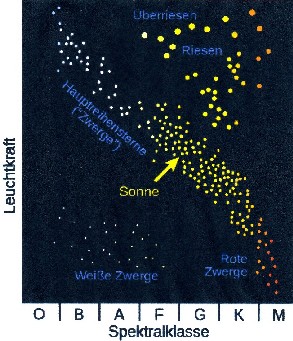 |
Die Sonnen
unserer Galaxie werden im sogenannten Hertzsprung-Russel-Diagramm
wiedergegeben, nach Farben und Leuchtkraft
angeordnet. Es existieren gesamt 13
Spektraltypen.
Wobei die Spektraltypen O, B,
A, F, K,
also die blauen, die blau-weißen, weißen, die
weiß-gelben und die orangen Spektralfarben etwa 1
% der Gesamtsterne ausmachen.
Hinzu kommen noch die Braunen Zwerge und die
roten Riesen, also die Spektralklassen L,
T, Y, R,
N, S, die
ebenfalls 1 % der Gesamtsterne
ausmachen.
Zwei Klassen sind bisher bekannt geworden. Und
zwar die Menge der sonnenähnlichen G-Sterne,
mit einer gelben Spektralfarbe und der
Wahrscheinlichkeit Fs
= 0,28 = 7:25.
Sowie die Menge der Roten Zwerge, also M-Sterne
mit einer rot-orangen Spektralfarbe und einer
Wahrscheinlichkeit FRZ
= 0,7 = 7:10. Damit machen die
beiden Spektralklassen 98 % der Gesamtsterne in
der Galaxie aus. |
|