Es lässt sich noch eine
Verfeinerung bei der Wahrscheinlichkeit der
Entwicklungshindernisse vornehmen.
Das Leben ist von q planetaren
Voraussetzungen abhängig.
D.h. sie bilden die Menge Q der
Entwicklungshindernisse.
Dann trägt jedes Element einen Beitrag zur
Gesamtwahrscheinlichkeit bei. Dieser Teil beträgt:
| 7.2.1 Gleichung |
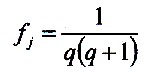 |
Es ist: 0 <
j < q + 1
Es gilt dann für die Gesamtwahrscheinlichkeit
der Entwicklungshindernisse
| 7.2.2 Gleichung |
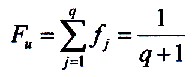 |
Eine Differenzierung der einzelnen Anteile erhält man
dadurch, dass man die einzelnen Elemente gewichtet.
| 7.2.3 Gleichung |
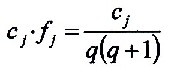 |
Dann ergibt sich für die Wahrscheinlichkeit der
Entwicklungshindernisse:
| 7.2.4 Gleichung |
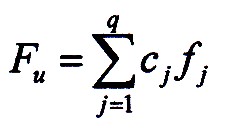 |
Insgesamt ergibt sich für die Wahrscheinlichkeit
der Entwicklungshindernisse:
| 7.2.5 Gleichung |
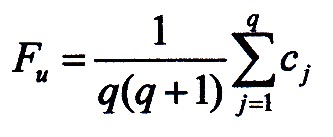 |
Gleichung 7.2.5 ist der allgemeinste Ansatz der
gemacht werden kann, für eine beliebige Menge Q von Entwicklungshindernissen, die in ihrer Einwirkung durch die cj
noch gewichtet
werden können.
In einem ersten Ansatz
wird davon ausgegangen, dass alle Teile gleichwertig
wirken, somit die Gewichtungsfaktoren alle eins sind,
also Gleichung 7.2.2 gilt.
| 7.2.6 Ansatz |
Die Gewichtungsfaktoren
werden gleich eins gesetzt
c1
= c2
= ... = cj
= ... = cn
= 1 |
Hier sind 5 Komponenten genannt die
Entwicklungshindernisse darstellen..
Es gilt für die Einzelwahrscheinlichkeit: fj
= 1:30
Daher können auch 5 Fehlschläge
auftreten.
Somit ist die Chance, dass Entwicklung entsteht 1
zu 6. Das entspricht einem Anteil von 16,66
%.
Der Wahrscheinlichkeitsfaktor für Entwicklung beträgt
demnach Fu
= 0,166... = 1:6.
Dieser Ansatz wird in allen folgenden Betrachtungen als
Grundlage der Berechnungen benutzt.
|