|
Bei den
bisherigen Betrachtungen wurden Sternsysteme
untersucht, die einen sonnenähnlichen
Zentralstern besitzen. Geht man davon aus, dass
auch andere Sternsysteme, also nicht
Sonnenähnliche, jeweils Häufigkeiten für
technologische Zivilisationen aufweisen, dann
lässt sich aus der Seager-Gleichung 10.3.2
ableiten: |
| |
|
| 12.1.1 Gleichung |
Nzx
= A · Fx
· Fph ·
Fk
· FLiz |
Die Gleichung 12.1.1 gilt dann für die Sternenmengen
die, jeweils durch einen Sonnentypus bzw. Spektralklasse
bedingt, gebildet werden.
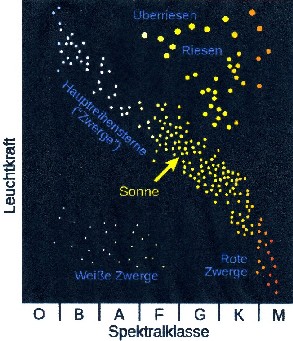 |
Die Sonnen
unserer Galaxie werden im sogenannten Hertzsprung-Russel-Diagramm
[2] wiedergegeben, nach Farben und Leuchtkraft
angeordnet. Es existieren gesamt 13
Spektraltypen.
Wobei die Spektraltypen O, B,
A, F, K,
also die blauen, die blau-weißen, weißen, die
weiß-gelben und die orangen Spektralfarben etwa 1
% der Gesamtsterne ausmachen.
Hinzu kommen noch die Braunen Zwerge und die
roten Riesen, also die Spektralklassen L,
T, Y, R,
N, S, die
ebenfalls 1 % der Gesamtsterne
ausmachen.
Zwei Klassen sind bisher bekannt geworden. Und
zwar die Menge der sonnenähnlichen G-Sterne,
mit einer gelben Spektralfarbe und der
Wahrscheinlichkeit Fs
= 0,28 = 7:25.
Sowie die Menge der Roten Zwerge, also M-Sterne
mit einer rot-orangen Spektralfarbe und einer
Wahrscheinlichkeit FRZ
= 0,7 = 7:10. Damit machen die
beiden Spektralklassen 98 % der Gesamtsterne in
der Galaxie aus. |
|